In this note the required strengths of the two chromaticity correcting sextupole loops are calculated.The work is not considered complete; therefore a significant portion of this note will describe the program used to produce the resulting sextupole curves, and the assumptions that have been used up to this point. It is intended that the program be straightforward in its application to the problem, and that any modifications to the assumptions made thus far can be easily incorporated.
The equations which model the chromaticity are:
![]()
and
![]()
Where S F and S D are the strengths of the chromaticity sextupole in units of (kg/m 2 ) - m (not B") and Sdip is the sextupole content of the dipoles (using the same units). The coefficients a, b, c, d, e, f, are the chromatic sensitivity coefficients to the changes in the corresponding devices. xnatH and xnatV are the natural chromaticities of the machine, and P is the momentum in GeV/c.
Although the current lattice is MI-15, the modeling of the Main Injector was done with MI-14. It is believed that this does not make a big difference in the results although it should be looked at.
The sextupole configuration is the one which I have used in all of my tracking studies. It has not been widely publicized, so I will mention it here. All fifty six cells have a sextupole at each quad. The rf insertions have sextupoles at each quad in the dispersion suppressing half cells, but not in the empty cells where the dispersion is zero. The transfer insertions have sextupoles at the quadrupoles in the adjacent half cells, and at the matching quads, there are sextupoles on the vertical loop. The numbers implied by this scheme are listed below.
Table 1: Sextupole count used in Determining Sensitivity Coefficients
| Beamline Section | Number of H Sextupoles | Number of V Sextupoles | Number of Beamline Sections | Total H | Total V |
| Standard Cell | 1 | 1 | 56 | 56 | 56 |
| rf Insertion | 4 | 4 | 2 | 8 | 8 |
| Transfer Insertion | 3 | 4 | 6 | 18 | 24 |
| MI-15 (Total) | 82 | 88 |
The four sensitivity coefficients corresponding to the sextupole correctors were found using both TEVLAT and SYNCH. The coefficients for the dipoles was found with TEVLAT. The values determined by these programs, and used in my program are:
Table 2: Sensitivity Coefficients
SYNCH |
TEVLAT |
Simple FODO |
Used in Program |
|
|---|---|---|---|---|
a |
.1122 |
.1104 |
.131 |
.111 |
b |
.0174 |
.0173 |
.0146 |
.0174 |
c |
|
.1686 |
.179 |
.1686 |
d |
-.0283 |
-.0282 |
-.0265 |
-.0283 |
e |
-.6653 |
-.0646 |
-.0725 |
- .0653 |
f |
|
-.1621 |
-.1628 |
-.1621 |
This section seems like the appropriate place to mention the natural chromaticities used; xnatH is -27.5, and xnatV is -28.4.
I have used three components of sextupole in the dipoles.
Sdip = Sremanent + Seddy + Ssaturation
For the remanent sextupole I used a constant value of
1.64 (kg/m 2 ) - m
This is added at all energies. Its value comes from existing Main Ring multipole
measurements on B2 style dipoles.
The eddy current term is proportional to j. As of this time
I have only used the results of Steve Holmes calculation in which he finds an eddy current sextupole of .24 T/m 2
with a ramp rate of 240 GeV/sec 1 . I have converted this to
14.5i'(kg/m 2 ) m for each dipole at the same ramp rate.
The saturation sextupole calculation is based on Stan Snowdon's note MI-800. On page 4, a table of sextupole content as a function of field is presented. For all practical purposes, only the highest three entries are of any use. I fit these three points to the following equation:
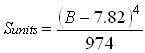
and for any field less than 7.82 kg, the saturation sextupole is set to zero. Note that this expression is in units; it is converted to (kg/m 2 ) m before being added to the other sextupole terms.
In writing this program I wanted generality, but I did not want to take the time to
write a high level ramp specification tool (along the lines of what a console program
might have). Thus I borrow the console format, but do not provide the high level entry
tools. For instance, if you want to add a slot in the middle of the parabola, you must
calculate the time, momemtum and ![]() by hand before entering them. A sample ramp file appears
below.
by hand before entering them. A sample ramp file appears
below.
| time | P | Pdot | Pddot | Cx | Cy |
| .l, | 8.9, | 0.0, | 0.00, | -10.0, | -10.0 |
| .172, | 9.62, | 20.0, | 277.78, | -10.0, | -10.0 |
| .28, | 15.02, | 80.0, | 556.56, | -10.0, | -10.0 |
| .312, | 18.149, | 115.57, | 1111.60 | -10.0, | -10.0 |
| .330, | 20.409, | 135.58, | 1111.60 | 10.0 | 10.0 |
| .42394, | 38.05, | 240.0, | 1111.60 | 10.0 | 10.0 |
| .5654, | 72.0 , | 240.0, | 0.0 | 10.0 | 10.0 |
| .68984, | 100.0, | 210.0, | -241.07 | 10.0 | 10.0 |
| .76984, | 116.0, | 190.0, | -250.0 | 10.0 | 10.0 |
| .81195, | 120.0, | 0.0, | -4512.5 | 10.0 | 10.0 |
| .9, | 120.0, | 0.0, | 0.0 | 10.0 | 10.0 |
The columns labeled Cx and Cy are not formally a part of the ramp specification, but are the requested chromaticites at those energies. The program linearly interpolates to determine the chromaticity to which it is correcting.
Having the above information, the program proceeds to solve the first set of equations for SF and SD . The time resolution is presently set to 3 milliseconds. Output is written to an intermediate file and the program "mongo" is used to make the plots.
The program and its supporting files are in:
/home/quad/rod/micalc
on the cartoon domain
| Source file: | sext-calc.f |
| Mongo command file: | mongosext .com |
| Ramp files: | ramp* |
A number of graphs are included with note. More will be forthcoming as our understanding of the magnets increases and as we move into more of an engineering design phase (where sextupole power supply currents and voltages will be of interest). Figures 1 through 5 use a 150 GeV ramp with an unrealistic final parabola. Five different chromaticity curves are represented. The maximum sextupole strengths which appear in these plots is for the case where both chromaticites are -20 units before transition and +20 units after transition. In this case the maximum horizontal sextupole strength is 450(kg/m 2 ) m and comes from the saturation sextupole. The maximum vertical sextupole strength is -411(kg/m 2 )- m and it is driven by the eddy current sextupole. It is also clear from these plots that, although it is tempting to suggest that unipolar supplies might be adaquate, the MI will need to have bipolar supplies.
Figure 6 uses a more realistic ramp with a slower ![]() near flattop. Although the
vertical sextupole is slightly less (-403(kg/m 2 ) - m),
there is no significant change.
near flattop. Although the
vertical sextupole is slightly less (-403(kg/m 2 ) - m),
there is no significant change.
New sensitivity coefficients have been derived for MI-15. The reason they are different from the MI-14 coefficients is not so much due to a change in the lattice, but a realization that the MI-15 design with the quadrupole centered in the ministraight allows more elements to be close to the quadrupole where the lattice functions are closer to the extrema. This uses all elements more effectively. Thus the lattice location for the sextupoles (which are zero-length elements in the models) has been moved to a point .45 meters downstream from the edge of the quadrupole. This in fact could be made closer as the engineering of these ministraights is better understood. The corresponding coefficients are:
Table A-l: Sensitivity Coefficients Revised for MI-l.5
| Used in Program | |
| a | .1175 |
| b | .0165 |
| c | |
| d | -.0174 |
| e | -.0666 |
| f |
Figure A-l shows the sextupole waveforms for the same ramp as in Figure 6. The maximum required strengths are now 425(kg/m 2 ) - m for the sextupoles at focusing quads and -386(Cg/m 2 ) - m for the sextupoles at vertical quads.
In configuring the sextupoles, twelve SD sextupoles had been placed around the long straight sections. This was done because of my concern about the lesser effect of the S D loop on chromaticity. However, this more complete analysis has shown that the SD loop does not need to be as strong as the SF loop. The sextupoles around the long straight sections may interfere with external beamlines, so there is motivation to get by without them. The sensitivity coefficients for the S D sextupoles have been recalculated with only 76 rather than 88 sextupoles. The results are:
Table A-2: Sensitivity Coefficients for 76 S D Sextupoles: MI-15
| b | .142 |
| e | -.0614 |
Figure A-2 indicates the needed sextupole strengths for this configuration. The maximum required strengths are 423(kg/m 2 ) - m for the sextupoles at focusing quads and -417(kg/m 2) - m for the SD sextupoles.
Phil Martin has released MI note 27 in which he specifies a standard ram for the Main Injector. It differs from the other ramps shown in this note in that it it only goes to 120 Gev/c, and it only has one parabola time constant prior to linear acceleration. The effect of this ramp on the sextupoles is shown in Figure B-1. The most notable feature of this change is that the maximum eddy current sextupole has moved earlier and now occurs at a momentum of 19.8 GeV/c where as before it occurred at 26 GeV/c. The magnitude is also greater; 8.1 units (at an inch) as opposed to 6.7 units.
I must include this appendix to admit that the results presented with regard to eddy current sextupole are incorrect. The number which I had previously used, 3.1 g/in2 is actually a B". Thus the eddy current sextupole reported up until now is twice the actual size. Figures A-2 and B-1 have been redone but the original figures A-2 and B-1 are still in the report so that the differences can be seen. Older Figures are not recalculated. The greatest effect of this change is on the sextupole content of dipole in the parabola. A smaller effect is on the needed strength of the vertical sextupole loop. It can be seen (Figure A-2) that the maximum strength of the vertical sextupoles is reduced from -417(kg/m2)-m to -394(kg/m2)-m.
1In versions of this note written before 7/24/90 I used the wrong value for the eddy current sextupole. See appendix C.